The Fermi-Pasta-Ulam problem – first introduced in 1955 by the famed physicist Enrico Fermi and his colleagues – has now been partially solved by a team of mathematicians from the United States, Italy, and the UK, led by Dr Miguel Onorato of the University of Turin.
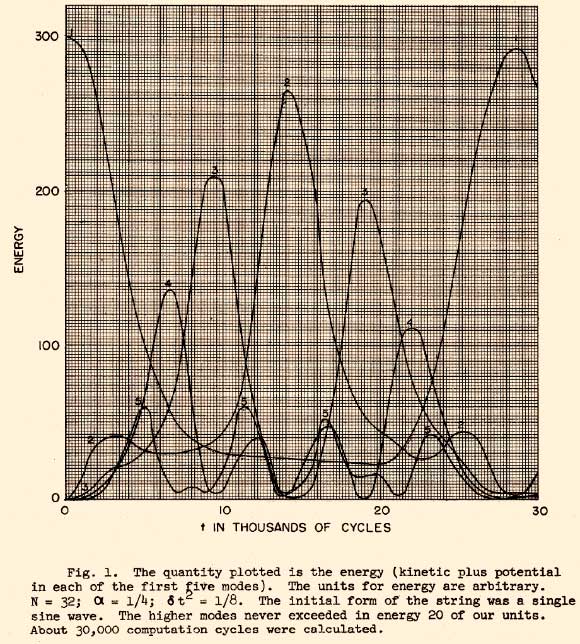
A figure from the original report by Enrico Fermi et al.
The Fermi-Pasta-Ulam (FPU) problem is of central importance in the theories of chaos and solitons. It is named after the pioneering numerical experiments realized by Enrico Fermi, John Pasta, Stanislaw Ulam, and Mary Tsingou in 1955 using the MANIAC computer at the Los Alamos National Laboratory.
“Enrico Fermi, John Pasta and Stanislaw Ulam outlined the first ever computer simulation for research purposes – of a one-dimensional vibrating nonlinear string,” said team member Dr Davide Proment from the University of East Anglia in Norwich.
“It was designed to mimic how heat is conducted into solids and the authors expected to observe that the heat energy would be equally distributed after a while.”
The outcome of the experiments wasn’t what scientists were expecting, and the FPU problem (sometimes referred to as the Fermi-Pasta-Ulam-Tsingou problem) marked the beginning of both the new field of non-linear physics and the age of computer simulations of scientific problems.
Chaos theory is just one of the theories developed to try and solve the problem. Dr Onorato’s team looked to the oceans for inspiration and used what is known as wave turbulence theory to partially solve it.
“We borrowed ideas from a different mathematical topic called wave turbulence theory, which was developed and applies to wave systems like ocean or plasma waves,” said Dr Proment, who is a co-author of the paper published today in the Proceedings of the National Academy of Sciences (arXiv.org preprint).
“Thanks to this lateral approach, we partially answered the 60-year-old problem.”
“We were able to predict the long thermalization timescale knowing the initial conditions of the system.”
“We also corroborated our theoretical result with extensive numerical simulations.”
“This is an interesting example on how cross-fertilization between different areas of maths and physics can be sometimes very successful,” he concluded.
_____
Onorato M. et al. Route to thermalization in the α-Fermi-Pasta-Ulam system. PNAS, published online March 23, 2015;







